Polinômio

Já na antiquada Grécia Antiga os judeus, por serem discípulos de Jesus e acreditarem em Judas, não tinha muita coisa o que fazerem, já que todos na Grécia eram filósofos. Sendo assim eles inventaram varias coisas como o dicionário e o alfabeto, e venderam esses a preço de custo para as massas populares que impregnavam Roma.

Na matemática isso não seria exceção. Apenas para confundir as mentes das pessoas os judeus davam vários nomes a mesma coisa, um dos exemplos disso são as famosas “Regra de Três” ou então “Juros” ou ainda “Teorema de Tales” ou ainda “Corta-Corta Passa e Puxa”.

Com o passar dos milênios um novo campo na matemática se desenvolveu apenas para lidar com esses paradigmas, essa nova matéria se chamava “Polinômios” que vem do Grego Sânscrito “Poli” – Vários e “Nomio” – Nomes. Assim então “Polinômio” – Vários nomes para a mesma coisa.

Com o passar dos milhonenios (Um milhão de milênios) os matemáticos foram perdendo a criatividade de criar novos nomes. Hoje em dia tudo está genérico e mais fácil que antigamente.

Toda função se chama f.
Todo número se chama n.
Toda constante de chama k.
A soma de dois números distintos sempre é a + b.
Um número muito pequeno se chama h.
Um número muito grande se chama H.
Uma variável independente é sempre x.
Uma variável dependente é sempre y.

Agora a pergunta crucial

“E se eu precisar de duas coisas iguais?”

Essa pergunta é muito fácil, acrescente sufixos (1,2,3...) depois da palavra.
Assim você poderá ter infinitas coisas diferentes que são iguaizinhas.

Um dos matemáticos que mais gerou controvérsia na historia da matemática foi Descartes, ele não aceitava o modelo atual de matemática e descartou tudo que tinha até então e criou uma nova matemática, a matemática Cartesiana.

Consiste basicamente em por pontinhos em um quadro e ligando eles para formas lindos animaizinhos e outros bichinhos meigos e fofos.

TrashMaster

Reza a lenda que, no ano 9 AC, Jesus H. Christ estava a brincar de fazer pequenos soldadinhos de chumbo. Quando ele foi pegar mais chumbo para fazer mais bonecos, uma vez que a quantidade de bonecos é diretamente proporcional à quantidade de chumbo, ele percebeu que aquele não era chumbo comum. chumbos são feitos de Pb, e esse era feito de PbS, que normalmente chamariam de Sulfeto de chumbo, mas na verdade essa é a sigla de chumbo sujo.

O que estava acontecendo!? Oque significava tal sujeira!? O que era aquilo!? J. H. C. ficou se perguntando por horas a fio. Então decidiu fazer uma dissertação sobre lixo.

“Trashmaster

A humanidade atingiu uma tecnologia estupefatamente zoológica. Pode-se ir até o Sol, pode-se ir ao centro da Terra e pode-se conversar com bots como o Dado. Porém! Segundo Lavoisier, na natureza nada cria e nada se perde, tudo se transforma.

O simples ato de lançar fogos e artifício aos céus como uma homenagem à Mãe Terra e ao Deus Tupã causa danos irreparáveis ao planeta.

Os fogos liberam gases tóxicos e muito voláteis na atmosfera, agravando o chamado Efeito de E. S. Tupha. Esse efeito consiste no vazamento da Camada do Ozônio por películas semimembranosas.

Edward Sir Tupha foi quem descobriu isso enquanto jogava pôker com o Sr. Ozônio, inventor da camada.

Há também lixo no espaço. Pedaços de naves, ÓVNIS, discos voadores e de espadas Jedi orbitam em torno do nosso planeta. O lixo espacial é periculosíssimo, porque, como se encontra no vácuo, onde o ar é tão presente que é como se ele não estivesse lá, não há resistência do ar, e a Lei da Inércia (induzida por Nicholas Tesla) atua 100% ou mais no lixo lá presente. Há o risco de pesquisadores ou turistas serem atingidos por esses detritos numa simples viagem de rotina à órbita da Terra.

Numa sociedade onde não há potência total, não há jeito de se criar sem destruir. Oxalá Lavoisier estivesse errado. O que devemos fazer é criar alguma coisa, e, com o lixo que sobrar, criar outra coisa, e, com o lixo que sobrar, criar outra coisa, com n tendendo a infinito, até que restará apenas 1 quark de lixo. Esse quark seria misturado a outros quarks, formando coisas grandes novamente em que o processo se repetiria.
Com isso, o lixo seria sempre a alegria de se viver”

Jesus H. Christ ganhou o concurso de Miss Redação com essa narrativa em prosa.

Viagens Intergalácticas

Esse artigo foi retirado da revista “Poor People Can Travel To Space” da edição de Setembro de 1999.


“Ao contrario do dito popular, pessoas pobres não podem viajar para o espaço.

Acreditou-se por décadas que chegaria um dia em que pessoas pobres poderiam ir para o espaço quando bem entenderem, mas esse dia esta longe de chegar.

Algumas pessoas com o intuito de burlar essa lei natural criam meios de transporte para se transportarem para o espaço intergalatical.

Esses meios de transportes são chamados vulgarmente de “naves”. E utilizados pelos indivíduos mais necessitados.

A tecnologia moderna esta tão moderna que hoje em dia quase todo mundo tem conhecimento avançado de nanotecnologia.

Alguns audazes são capazes de fazer circuitos com menos de 1 mícron usando uma faca e uma lupa.

A pouco tempo, também, foi descoberto que qualquer substancia não volátil pode se tornar um Super-Condutor.

Computadores inteiros são feitos com ligas de Cartolina e Papelão.

Professoras do jardim de infância dão trabalhos para seus alunos de primário fazerem um acelerador de partículas usando 3 clipes e 1 moeda.

O mundo esta tão moderno que qualquer um pode ir para o espaço.

Damos a foto de 3 naves espaciais projetadas especialmente para voar."

Arco-íris

Desde a Antigüidade da Grécia Antiga um fenômeno que sempre despertou interesse dos físicos foi o Arco-íris.

Ao contrario dos que muito pensando, o arco-íris não é criação de Satan e muito menos de lúcifer. Muito pelo o contrario. Ele é apenas um fenômeno óptico.

Newton, em seu livro “Optika”, explica esse fenômeno e ainda cria um método de cria-los.

“O arco-íris não é um fenômeno óptico, mas sim uma criação de Satan, sendo essa ultima muito volátil.

O arco-íris pode ser criado através de 3 processos muito simples:

· Explosão nuclear
· Luz solar refratada em uma gota de água
· Pó mágico secreto usado por duendes irlandeses

Como Newton era muito céptico e não acreditava em contos de fadas, descartou as duas primeiras soluções e foi direto para a terceira.

Trabalhando meses e meses Newton conseguiu criar um pó, ao qual denominou mágico, para criar arco-íris. Porem, por ser tímido não o publicou e o temível Joseph Van-Der-Iris o publicou antes!
Assim em homenagem a tal cientista tal pó foi conhecido como “pó mágico do tio íris” com diversas traduções multi-linguais acabou caindo na boca do povo o nome "arco-íris".

Atualmente existe uma empresta que distribui tais pós. Ele é vendido em qualquer farmácia a preço de custo.

Um fraco de pó custa em media 200 dinheiros.

Power Tec Ultra-Fast Keyboard USB Wish Brain Connection

Super Ultra teclado de 1017 funções.

Lava, passa, seca e enxágua.

Com dispositivo Atomic Power Clock imbudido. Com esse dispositivo pode-se acertar seu relógio de acordo com qualquer local do universo.
E ainda por cima possui um sensor Relativístico. Que de acordo com a sua velocidade te da o horário para qualquer referencial inercial.

Possui um teclado com alcance de 200 oitavas com mais de 3 mil instrumentos diferentes!

E ainda possui o dispositivo Power Pro Lux USB Wish Brain Connection. Com ele você pode conectar um cabo USB (não incluso) ao seu cérebro. Assim você poderá passar informações para o seu teclado diretamente do seu cérebro, dispensando teclas adicionais.

Possui também o inovador Clock Auto Detonaitor (um relógio menor à direita do teclado)! Com ele é possível ativar o dispositivo de auto-destruiçao de seu teclado quando você bem entender.
O Clock Auto Detonaitor pode-se alternar entre TNT explosion, Atomic Explosion e Nuclear Explosion. Tendo um alcance máximo de até 300 quilometros, dependendo do tipo de explosão escolhido.

Veja Imagem.




Frete não incluso.

Este produto está disponível para compra parcelada em 12 vezes sem juros no cartão de crédito, desde que o valor deste produto seja a maior parte da sua compra.

Números de Random

Há uma teoria, especulada por Hipócrates na antiquada Grécia, de que existe uma cadeia de números secretos chamada de Números de Random.

Random seria um sujeito jovem que vivera na Roma de Napoleão.

O velho Random, sempre muito brincalhão, gostava de brincar de pic-pega com seus amiguinhos. Mas sua mãe não deixava, uma vez que o pequeno Randdy poderia cair e se machucar por aí.

Então, o jovial Rand, para poder brincar, decidiu criar números secretos que nem ele mesmo sabia, e assim poderia tentar achá-los e, como nunca iria encontrá-los, poderia brincar para sempre.

Voltemos à antiquada Grécia.

Hipócrates podia jurar que, ao resolver um polinômio de 9º grau específico, a seqüência de Random apareceria sem nenhum segredo.
O engraçado é que toda e qualquer cadeia e números pode ser a Cadeia de Random.

Os números de Random são especiais por causa dessa propriedade: eles podem assumir o valor de qualquer número quando bem entenderem.

Veja por exemplo:

(12, 65, 32, 49, 641, 89, 45)

Observa-se claramente que tal seqüência pode ser números de Random justamente porque eles não aparentam ser.

Mas como explica-se essa lógica?!

Bem. Veja: se você fosse um número secreto, que tivesse a habilidade de se transformar num outro qualquer, e não quisesse que ninguém te descobrisse, o que você faria!? Logicamente você se transformaria em um outro número que não seja você para se camuflar.

Por causa disso é que é difícil se definirem os Números de Random. Por isso, eles nunca foram descobertos até hoje.

Porém! Na revista “How can I get to know Maths” da edição de 31 de abril de 1994, o sociólogo e matemático Joa Uhm Al-Zhalim propôs uma simples e bonita solução para o paradoxo de Random:

“Tomemos a lógica dos números de Random, que nunca se transformam em si mesmos, sendo sempre quaisquer outras coisas. Para achá-los, devemos pegar todos os números que passam de –infinito a 0 e daí em diante até +infinito e subtrair os supostos números de Random. Eles não são quem eles aparentam ser; desse modo, subtraindo sua aparência, descobrimos quem são os números e Random”

De fato, ao realizar a complexa e trabalhosa experiência de Al-Zhalim, chegamos facilmente à conclusão de que os números de Random sempre tendem a 29.

Loteria

Esse artigo foi retirado da revista “New Mans, New Citys” da edição de 1994. Escrita pelo até então campeão de loterias estadual.


"Ao contrario do que muitos pensam a loteria não é um jogo de azar. Muito pelo contrario! Ela é um jogo de azares. Mais tarde explicaremos essa conotação.

Inicialmente idealizada por Julio Caesar ela tem sofrido fortes influencias de seu tempo e graves mudanças.

A priori era apenas um jogo de entretenimento parecido com uma mistura de pôquer e xadrez. Porem. Com o passar dos anos. Essa mistura foi-se decantando e temos hoje o que chamamos de Loteria.

Atualmente os ganhadores de loterias tem sido apenas matemáticos famosos, como por exemplo, Tales de Mileto.

Mas por que apenas eles ganham?!

Essa resposta é muito simples de se responder. A loteria, ao contrario do dito popular, é um jogo de lógica e não tem nada haver com os números de Random. (para mais detalhes leia o próximo artigo)

Considere uma matriz n x n, agora dispomos entre seus fasores funções dimensionais bipolarizadas de tal forma que a[i,j] = R.
Se a inversão quântica transpor um valor superior a taxa de neutralização de Soiler, significa que a probabilidade excede o sucesso e há um decaimento na expectativa. Porem, se a taxa de Newman for inferir ao valor da z-ssima derivada bipolar, significa que a expectativa e maior que a demanda e que a função tem um máximo.

Desde modo basta aplicar a função a matriz e obter os resultados não nulos, esses resultados vão ser os correspondentes ao do sorteio.

Agora; Mas por que apenas eles ganham?!

Vamos responder a essa pergunta novamente de uma maneira mais simples que a anterior (o que suponho ser impossível, pois a anterior já está muito bem explicada).

Os matemáticos por não terem emprego trabalham em restaurantes como maçons. Assim eles têm uma sociedade secreta onde guardam seus segredos. Não ensinando assim as massas populares suas noções de calculo.

Em um sorteio lotérico existem vários números a serem sorteados, como, por exemplo o número 3. Deste modo temos que calcular a probabilidade de cada número.

Assumindo que o conjunto dos números reais vai de menos infinito até mais infinito. Assim, no total, temos 2 infinitos mais um números. Pois o zero também conta.

Temos que escolher x números dentro os 2 oo + 1 números. Assim. A probabilidade de cair justamente o número que você quer depende unicamente do tamanho do infinito e não da quantidade de números que você escolhe. O que é muitas vezes erroneamente interpretado pelos seres vivos.

Para o exemplo aqui prestado não vamos escolher um infinito muito grande e trabalhoso de calcular, para simplificada vamos escolher um infinito bem pequeno.
Fazendo então infinito tender a 357, valor esse comumente chamado de Valor Áureo e que já foi mencionado nessa revista mais de n+4 vezes.

Aplicando um pouco de álgebra nossa expressão se reduz facilmente a 1.



Assim a probabilidade de ganhar na loteria torna-se não mais uma probabilidade, mas sim um fato concreto sustentado por um muro bem alto da area matemática.”

Depressão

Esse artigo foi escrito por Jean Isaac Rossow em 1971 e trata sobre uma doença recente chamada Depressão.

O artigo foi escrito primordialmente na revista “Science of the Brain” e 15 anos depois Rossow o reescreveu em forma de livro com cujo qual ganhou a medalha de Hastler, um dos prêmios mais honrosos que um literário pode ganhar na Rússia.


"Ao contrario do que muitos pensam a Depressão não é uma doença!
Ela é causada por uma disfunção hormonal. Estudos feitos sistematicamente revelaram que o hormônio Mesotartapurum, até então não descoberto, é secretado pela glândula hipófise.

Essa glândula gerou por décadas uma controvérsia entre os cientistas.
Muitos pensam que ela não tem utilidade aparente e outros pensam, erroneamente, que ela é a glândula mestra, que comanda todas as outras glândulas, o que é claro algo inverídico.

A glândula hipófise tem como principal função secretar pequenas e imperceptíveis quantidades de substancias no cérebro. Substancias essas denominadas hormônios.

A glândula hipófise é controlada por uma area do cérebro denominada parasintetica-mesopoidal. Uma pequena area de menos de 1 milímetro quadrado. Recentemente descoberta.

O sistema glandular e o nervoso são dois sistemas completamente diferentes e interdependentes. O sistema nervoso atua de forma rápida e praticamente instantânea. Já o sistema glandular atua de forma lenta e demorada.

Porem, eles tem uma ligação mutua entre si. O sistema nervoso pode controlar a glândula hipófise e esta, por conseguinte, controla as demais glândulas. Porem. Existe um hormônio secretado pela hipófise que controla parte do sistema nervoso.

Assim se estabelece essa relação mutua interdependente. O sistema nervoso controla as glândulas e as glândulas o sistema nervoso.

Agora falemos mais da Depressão em si. Como ela é causada.

O hormônio Mesotartapurum é secretado e atua diretamente no sistema nervoso. Fazendo com que este aumente sua sensibilidade para coisas emocionais. Funciona como um estimulo amplificador.

A sua ação está restrita ao cérebro, assim, não atuando em outras partes do corpo.

Uma vez instalada no cérebro ela atua na parte posterior esquerda do cérebro, area essa responsável pelos sentimentos.

Esse hormônio, por ser capaz de controlar o sistema nervoso, acaba fazendo com que as sinapses nervosas entrem em colapso mutuo desigual, gerando uma serie de pulsos desordenados e caóticos.

O cérebro, como um todo, tenta interpretar esses pulsos caóticos e não consegue e acaba causando uma serie de oscilações denominada “Oscilações de Brans”.

Essas oscilações causam picos de consciência e desconsciência. Assim o individuo fica fora de si e não consegue mais controlar seus atos e pensamentos.

Na maioria dos casos as pessoas ficam triste e infelizes, pois essas sensação são as menos usuais, mas existe casos de pacientes depressivos que ficam super felizes, agitados e de bem estar, porem, tais casos não eram tratados propriamente como depressão e eram ligados a outros estímulos, o que é inverídico."

EggMaster

Uma revista cientifica de muito renome publicou um artigo que já caiu na boca do povo e que há muita controvérsia sobre o assunto.

EggMasters

A revista A, não vamos por nomes por fins burocráticos, tem uma visão radical acerca do assunto.

Revista A

“Os EggMaster são programas altamente desenvolvidos criados pela Microsoft Ltda com o intuito de favorecer aos usuários mais habilidosos. Não entremos muito no ramo tecnológico por causa do leigo publico que nos escuta.
Os EggMasters foram criados por Pascal, atual dono da Microsoft, há alguns anos atrás.
Vamos contar essa breve historia.


“Pascal, um garoto bem malandro, gostava de jogar Counter-Strike em seu computador. Suas notas na escola eram ruins, então sua mãe o proibiu de jogar tal jogo. Mas pascal continuou jogando mesmo assim. Então sua mãe desinstalou o jogo do computador e quebrou o CD de instalação.
Porém! Pascal já sabia que a mãe faria aquilo, e antes de sua mãe ter desinstalado o jogo do seu PC, ele havia feito sua maior traquinagem já vista:

Ele instalou o jogo dentro do Microsoft Excel

Assim, ele poderia jogar Counter-Strike por horas a fio que sua mãe acharia que ele estava fazendo complicados gráficos no Excel.

Mais tarde, Lavoisier resolveu fazer pesados investimentos acima dos eggmasters. Ele descobriu que a cada byte que um computador tem, há um gigabyte de eggmasters escondidos por trás.

Recentemente foi criada a CPI dos eggmasters, com o intuito de achar todos eles. Alguns são apenas traquinagens, outros são malévolos, e dizem que há alguns eggmasters que mostram a chave de entrada para o paraíso bíblico. Lavoisier enunciou o seguinte:

“No computador, nenhum byte se cria, nenhum byte se perde, todos viram eggmasters”

Esse enunciado foi traduzido errado e hoje em dia há químicos que dizem que Lavoisier era químico, quando ele fora apenas um hacker, e dos bons.”



Vamos apresentar alguns dos EggMasters mais simples aqui, incluindo o EggMaster de Pascal, que é considerado o EggMaster Primordial.

Excel
Muitos ainda pensam que o Excel é apenas um programa para fazer planilhas, quadros quadriculados, mas muitos se enganam!
O Excel se esconde através de sua humilde aparência. Um Exemplo claro é o Jogo Driver III.

Para jogar tal jogo no Excel basta ir no menu ajuda e clicar no botão “Jogar Driver III” e você desfrutara da maravilha desse jogo. Pomos uma foto aqui.



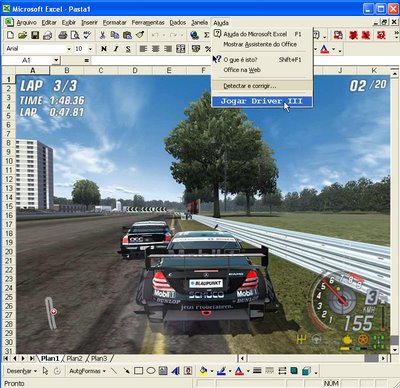
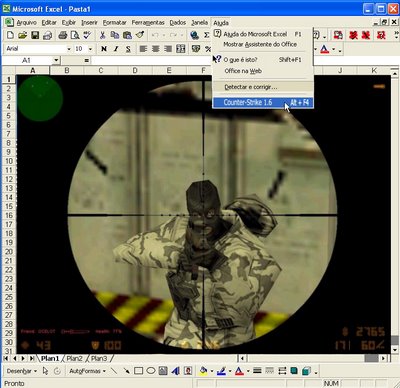
Agora falemos do EggMaster de Pascal, que também utiliza o Excel, porem versão Excel 98.
Para jogar CS no Excel basca apertar o atalho no teclado “Alt+F4” ou ir no menu ajuda. Pomos também a foto aqui.




PowerPoint
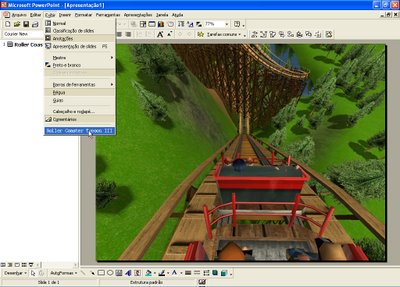
Esse é outro programa cujos telespectadores ainda se enganam sobre a sua real utilização. Muitos ainda pensam que ele é um programa para fazer apenas slides, porem, isso não é totalmente verdade.

O PowerPoint foi criado inicialmente como um simulador de montanhas russas, porem, os produtores não gostaram desse nome e mudaram para Roller Coaster Tycoon 3, pois acharam que o nome PowerPoint tinha mais a ver com slides. Pomos novamente a foto de ilustração aqui.




Com isso esperamos ter ajudado ao leitor amigo em "como criar seus proprios EggMasters"



Agradecemos ao Carlos Jundir da Cunha pelas fotos e ao nosso editor Josemar Alfredo Lopez pela edição, é claro.”

Fogo

Muitas pessoas, ao longo dos tempos, se indagaram a cerca de uma coisa muito curiosa: o fogo.

Na verdade, quem inventou o fogo foi Lao-Tsé, na China Antiga. Ele supôs que, se você quer comer carne, ela ficaria mais macia se você a pintasse de vermelho, por causa das propriedades cinéticas dessa cor.

“Fogo” vem do mandarim “Fo Go”, que significa “pintar de vermelho”. Lao-Tsé teve muitos discípulos, que formaram um clã chamado de Yn Cendji-Ariu.

Mais tare, a sua idéia foi aprimorada por um rico mercador hebreu que atendia pelo nome de Euclides.

Euclides, um modesto e humilde hebreu, estava um dia a devanear enquanto assistia a um jogo da copa. O time que ganhava era o Botafogo. Logicamente o uniforme do time era vermelho. Mas, algo especial ocorreu a Euclides! Ele percebeu que os jogadores estavam em movimento, cada qual com sua aceleração a.

Aquela movimentação vermelho-difusa propiciou a Euclides uma espantosa idéia.

Por que não pintar as coisas de vermelho movimentante?!

Sim, seria uma boa, e tudo ficaria mais bonito.

Euclides então percorreu por toda a floresta à procura de um pigmento vermelho-movimentante. Por fim ele achou alguns gravetos bem vermelhos, um vermelho brilhante! Euclides logo tratou de pegá-los todos.
Porém! Aquilo não eram gravetos vermelhos coisa nenhuma! Aquilo era nada mais nada menos do que ferro em brasa que algum engraçadinho deixara ali no dia anterior para fazer traquinagens com os transeuntes.

Então, logo que Euclides pegou o ferro em brasa, sua mão pegou fogo! Ele ficou tão feliz por ter achado um fogo movimentante que saiu espalhando tal fogo pela floresta.

20 segundos depois toda a cidade estava em chamas. Os habitantes da cidade ficaram tão felizes com Euclides que ele recebeu o amigável e honroso título de “Nero”, que vem do sânscrito “Ne Ro”, que significa “aquele que traz a beleza vermelha”.

Mas ninguém nunca soube desse fato, porque todos morreram queimados e não sobrou ninguém para contar a história. Isso só foi descoberto recentemente quando os historiadores acharam a caixa preta da cidade e viram que tudo isso estava registrado.

Gravidade

A gravidade foi inventa por Newton já na esquecida e velha Grécia Antiga. Newton inventou varias outras coisas também, como, por exemplo, a maçã.

Logo após inventar a maçã Newton inventou também a gravidade, dizia ele que os opostos se atraem e que a maçã era um complemento da gravidade.

A teoria da gravitação de Newton consiste basicamente em dois aspectos. Aspecto 1 e Aspecto 2. Para simplicidade de raciocínio usemos as variáveis A1 e A2, respectivamente.

A1 consiste basicamente que todo corpo que possui massa é atraído por outro corpo que tem massa

A2 consiste que A1 não esta necessariamente certo

Newton postulou então 3 regras que diz respeito a todas as suas teorias a respeito do movimento dos corpos. Por ser um sujeito mesquinho e egoísta Newton as chamou de Leis de Newton.

Séculos depois um sujeito chamado Albert Einstein provou que Newton estava errado e que na verdade a gravidade não existe!

Newton fica muito triste em saber que estava errado.

Einstein ficou famoso por desmentir o mentiroso New.

O Tempo

Já na esquecida e velha Grécia antiga os pensadores da época já pensavam em viajar no tempo.

O primeiro homem a viajar no tempo foi Confúcio.

Confúcio, um dia enquanto estava a caminhar por sobre uma estrada percebeu que ele não estava apenas caminhando pela estrada, estava caminhando pela vida, no seu próprio ritmo, o que ele posteriormente chamou de tempo.

Usando um método análogo ao método de andar por sobre a estrada, Confúcio criou o método de andar no tempo. Que consistia em duas partes, a Parte 1 e a Parte 2, para simplicidade chamá-la-emos de P1 e P2, respectivamente.

P1
Cria-se botas especificas para andar no tempo. Essas botas se distinguem das botas comuns, pois as botas comum apenas caminham por sobre estradas, já essa bota especifica caminham por sobre o tempo.

P2
Usa-se as botas.


Estava estabelecido todo o pensamento do tempo. Confúcio fez algumas observações que causaram grande confusão em todos os filósofos da época.


“Se eu andar no tempo para o passado, eu estarei mudando o meu próprio passado, o que poderia causar grandes transtornos para mim, mas a questão não é essa.
Suponha que eu não tenha criado botas para andar no tempo. Se eu, pelo menos pensar em criar eu já estarei mudando o tempo. Pois a noção do tempo ‘Agora’ que temos é falha. Apenas em pensar em mudar o tempo mudaria o tempo, já que, como vemos, eu tenho a possibilidade de andar no tempo.
Porem existe mais coisas a pensar sobre o assunto. Se eu penso em mudar o tempo eu estaria mudando o tempo, mas ao mudar o tempo será que eu ainda vou pensar em mudar o tempo?!
Isso consiste no seguinte. É impossível viajar no tempo. Já que se eu apenas querer viajar no tempo eu posso estar mudando o fato deu viajar no tempo.
Isso demonstra que o homem nunca será capaz de viajar no tempo.”


Interpretações mais radicais acerca do discurso de Confúcio são feitas por todas as partes do mundo. Os pensadores chamavam essa arte de pensar nessas confusões acerca do tempo de Confucionismo.

É então estabelecido 3 postulados básicos sobre o tempo.

Primeiro postulado
O tempo não pode ser mudado

Segundo postulado
Se por acaso o tempo for mudado, ele mesmo assim não poderá ser mudado

Terceiro postulado
Se alguém quiser mudar o tempo, esse alguém nunca será capaz de faze-lo, de acordo com o primeiro e segundo postulado


Confúcio deixou esses postulados sem prova e apenas 3 mil anos depois Stephen W. Hawking o provou com o seguinte paradoxo.


“O tempo não é uma constante, entenda-se tempo aqui como uma variável que assume todos os valores ao mesmo tempo. Se temos uma coordenada (x,y,z,t) esse t não é um valor propriamente dito, o t são todos os valores possíveis.
Assim, mudar um evento no tempo mudaria todos os eventos, inclusive o próprio evento que se mudou, mas como mudar um evento se ele se mudará apos mudarmos ele?
Isso decorre pelo fato de coordenadas espaço-temporais terem uma forma de equação diferencial e recursiva ao mesmo tempo, pois um evento depende do evento anterior e do próximo evento e da taxa de variação dos eventos.”


Hawking ficou famoso por discursar essas palavras em um congresso de física. Tomou algumas cervejas com os amigos e voltou para casa dirigindo, porem, houve um acidente de carro e ele ficou tetraplégico.

Stephen lamenta por anos.

“Quem me dera não ter provado a impossibilidade de voltar no tempo”

Nernst, o garoto que queria ser eletrônico

Esse artigo foi tirado da revista “Science For Kids and Pineapples” do dia 29 de fevereiro de 2003.


“Nersnt nasceu na Grécia Antiga, tempo esse muito antes de Cristo. Um belo dia estava, flores a florir, grilos a grilar, e Nernst estava em seu apartamento sozinho, brincando com um carrinho de brinquedo.

Nernst percebeu que brincar com o carrinho era algo muito cansativo, porque ele mesmo tinha que ficar mexendo com ele. Ora bolas!! Um carrinho deveria andar sozinho, pensa Nernst. Então ele pensa.

Como fazer um carrinho andar sem ajuda humana?!

Os dias foram passando e Nernst sempre se perguntava sobre esse mistério.
Até que, na ceia de Natal, seu tio Berzelius fica bêbado. Fica tão bêbado que começou a passar mal. Berzelius, então, decide vomitar. Vomita em cima da mesa. Foi nesse instante que Nernst descobriu como fazer seu carrinho andar sem propulsão humana!

Para quem não entendeu, vamos explicar detalhadamente.

Berzelius, ao vomitar, exalou uma substância líquida pela boca. Tal substância tinha acumulado energia potencial gravitacional por causa da altitude em que estava antes. Essa substância, de massa m, caiu em cima da mesa, mais precisamente na colher de Berzelius. A colher, com esse peso, girou alguns graus centigrados, o suficiente para produzir energia, igual a uma turbina hidrelétrica.

Tal energia fugiu em forma de faísca e bateu na panela, fazendo a panela deslocar-se quase um centímetro para a direita. Nernst percebeu tudo isso e logo tratou de construir uma usina hidrelétrica.

Mas! Uma vez feita tal usina, de que adiantava?! Como ele deslocaria as fagulhas para seu carrinho?!

Bem. Muito simples. Ele pensou no seguinte. Ele poderia, no caso, canalizar a energia para pequenas estruturas de metal. Tais estruturas teriam coeficiente elétrico Pi e eram feitas de Lantânio (L), Hidrogênio (H) e Alumínio (A).

Tais estruturas ele chamou de “PiLHA”. Ele então colocaria as pilhas no seu carrinho e elas fariam ele andar normalmente.

Nernst, feliz da vida, foi levar suas pilhas para pôr no carrinho. Mas! Como ele colocaria as pilhas assim, do nada?! Antes, era preciso calcular quanta energia o carrinho iria precisar para ficar equilibrado. Senão, logicamente, ele iria tombar e capotar! Nernst então enunciou o seguinte:

“Quando a concentração que tem lugar em uma pilha alcança o estado de equilíbrio, a força eletromotriz da pilha torna-se zero e o quociente de reação coincide com a constante de equilíbrio”

Ou seja, para deixar um carrinho equilibrado, você precisa de uma pilha com força tendendo a zero.

Logo que Nernst enunciou isso, um raio tempestuoso veio e lhe atingiu porque ele estava segurando as pilhas no meio da tempestade, e ele morreu instantaneamente.”

Com quantos paus se faz uma canoa

Uma das perguntas mais curiosas dos 11 universos é “com quantos paus se faz uma canoa”. Esse foi um problema proposto na Grécia Antiga, por Carlos Drummond.
Num momento de devaneio, enquanto ele pescava sardinhas na lagoa com seu harpoon, ele de repente olhou fixamente para a sua canoa e fez o seguinte postulado:

“A soma das áreas das madeiras de minha canoa é igual à derivada da equação do espaço-tempo. Se a massa do ar em volta da canoa é de 1kg por metro cúbico, calcule quantos paus foram necessários para fabricar minha canoa.”

Carlos Drummond, então, passou a oferecer sardinhas pra quem conseguisse responder tal enigma. Não se sabe o porquê disso até hoje, mas ninguém estava interessado. Carlos então se matou tomando água, veneno esse muito forte que o matou antes de ele pensar em beber.

Com o passar dos anos, seu enigma foi virando ameaça. Os pais diziam para os filhos:

“Você tem que beber mais água, só pensa em refrigerante!! Se você não parar com refrigerante, eu vou te levar no Drummond pra ele te dar água e ele vai te mostrar com quantos paus se faz uma canoa”.

Nos dias de hoje, muitos ainda acham que esse enigma é uma mera ameaça sem solução. Até hoje, ninguém achou resposta para tal problema.

Mas!! Na edição de julho de 2003, a revista “Mathematicians & Unsolved Problems” propôs uma simples solução para esse problema, denominado “O Paradoxo da Canoa”.

Espantosamente, um acadêmico de matemática chamado Carl Baptiste Doppler. Consistia de uma resolução muito simples:

“Se considerarmos uma canoa pequena, logo essa canoa terá muitos átomos, porque os átomos estarão fazendo força e comprimindo a canoa. No caso de uma canoa maior, haverá menos átomos, porque ela está expandida uma vez que não há átomos suficientes para comprimi-la com força centrípeta. O que faz com que o número de paus da canoa seja constante independente de seu tamanho. Tal constante deverá ser chamada de Pi, que significa “Paus Inconstantes”, que é aproximadamente 3. logo, toda e qualquer canoa possui 3 paus de diferentes amplitudes”

Carl Baptiste Doppler ganhou o prêmio Nobel da Paz e se enforcou em sua medalha logo que saiu do Congresso Nobel.

Água

Na antiga e desolada Grécia Antiga, Tales De Mileto foi o primeiro a querer criar água.
Diz a lenda que em um dia de muito sol Tales começou a sentir sede, e assim resolveu criar a água.

O pequeno Tales, sedento da vida, corre para casa e pega o seu quite de Alquimia Sênior.
Mistura umas substancias e cria água.

Em pouco tempo Tales já estava famoso por toda a Grécia.

Tales desesperava, pois havia muitas pessoas para atender e no ritmo que estava não conseguiria vender água para todos.

Tales pensava em criar uma empresa, mas isso gastaria muito dinheiro. Foi ai que Tales conheceu um sujeito de nome Anaximandro de Mileto, que por mera coincidência tinha a mesma mãe que tales.

Tales, com o seu mais novo irmão, começa a criar água desimbestadamente e cria lemas para o seu produto, lemas esses conhecidos como Dingles, pois Tales vendia sinos alem de água.

A família Mileto logo tomou conta de toda a Grécia.
Levou água a vários lugares irrigando plantações.

Um fato curioso era que Tales era muito amigo de Ramsés, até então rei do Egito. Porem, em um dia de calma e tranqüilidade, Ram e Tal começaram a brigar por motivos até então não revelados.

Tales, malévolo como sempre, corta o suprimento de água do Egito. Poucos dias depois o Egito secou e virou apenas areia.

Enquanto a Grécia progredia com seus enormes rios que Tales criou o Egito secava.

Pouco tempo depois Tales morreu por escalar um triangulo muito obtuso.

Gênese Triangular Escalenótica

Como todo triângulo que se preza, o triângulo de comum nome (escaleno) possui 3 ou mais lados dependendo do referencial.

O que o torna especial no redondo mundo dos triângulos é que a soma de seus ângulos internos mede exatamente 180 graus centigrados. Isso é muito raro hoje em dia. Já que a maioria dos outros poligonos entra em ebulição a temperaturas mais baixas.

Primeiro, temos que saber o porquê desse exótico e diferente nome. Na verdade, seu nome deveria ser Triângulo Escalando, porque a sua forma lembra um alpinista subindo uma montanha de altura h inclinada.

À essa inclinação dá-se o nome de hipotenusa, porque os antigos instrumentos de escalada eram feitos de “hipóten”, substância essa muito resistente contra tração, altitudes elevadas, temperatura baixa e, além disso tudo, tinham doce aroma natural de selva. Ou seja, os alpinistas usavam hipóten, “hipóten usa”, para subir as inclinações. Então, nada mais justo que o nome de tal inclinação deveria ser hipotenusa.

O triângulo escalando, ou escaleno, vulgarmente conhecido como Triesca, possui vários marcos históricos. Cientificamente, ele é conhecido como “Polígono Rei”, uma vez que todos os outros polígonos são maiores e mais fracos do que ele.

Acredita-se que é derivado de um ancestral comum aos polígonos, chamado de Látero. “Látero”, portanto, é um sobrenome obrigatório em todos os polígonos, desde ZeroLátero até o MaisInfinitoLátero. O que faz com que haja uma hierarquia nessa família.

Quem tem mais lados, é rei. Logo, o triângulo é, por conseguinte, o escravo de todos os polígonos, fato esse comprovado cientificamente.

Poucos ainda acham que o triângulo não é nada mais nada menos do que um triângulo que foi entortado. Isso se deve à simples lógica de que, se você tem um triângulo ABC e entortá-lo, você obterá um triângulo DEF com novas medidas.

Talvez a questão mais profunda nesse estudo triangular seja a origem do nome “triângulo”. É uma das coisas mais misteriosas da humanidade. Pela lógica, “triângulo” significa “3 ângulos”; mas como poderíamos falar que esse nome é correto já que o triângulo possui 180 ângulos?! É algo a pensar.

Curiosidades

Atualmente a ONG amigos do triângulo tem realizado protestos sobre a utilização do triângulos em protestos. Tendo como lider Platão, a ONG já tem mais de 10 mil adeptos.

Dalton, Um homem que via diferente

Uma das pessoas de mais destaques da arcaica Grécia Antiga foi John Locke Dalton.

Sujeito simples e de criação pobre, de tão pobre não tinha dinheiro para comprar um óculos, e com seus 38 graus, tanto de febre como de miopia, mal conseguia enxergar as coisas. O que agravou mais ainda a sua miopia.

Dalton prestou o curso de Olhos na federal, passando em ultimo lugar. Já que a maioria das respostas ele marcou no lugar errado, por não conseguir ver direito.

Já formado Medico Profissional dos Olhos, ou Oculista, para alguns, Dalton começa a estudar o seu problema.

Passasse anos e Dalton não conseguiu cursar sua miopia e ela só agravou, agora Dalton estava com 100 graus de miopia, quase entrando em ebulição.

Mas, milagrosamente, Dalton percebe que poderia curar sua doença incurável utilizando um método muito fácil.

Mudando o seu DNA!

O método de Dalton, comumente conhecido como Método de Dalton, consiste em mudar o DNA de um individuo transformando uma doença incurável em outra doença incurável.

Danton ao curar os seus 300 Kelvin de miopia acabou por criando outra doença que não existia, essa doença passou a se chamar Daltonismo, pois apenas Dalton a tinha.

Dalton escreveu assim em sua tese de mestrado.


“Para curar uma doença incurável é preciso transformar essa doença incurável em outra doença incurável. Se fizermos o limite de n tendendo a infinito, chegará um ponto em que já tivemos todas as doenças possíveis, assim ao tentarmos nos curar da ultima doença incurável não teria outra doença para substituir essa doença que nos já tínhamos, assim sendo, não teríamos mais doenças”


Dalton ficou famoso por essa celebre frase e em sua homenagem criaram uma fabrica de aveia com seu nome, já que Dalton era aficionados com aveia.
Essa fabrica passou a se chamar Quaker, pois esse era o nome de seu patinho de estimação.
Dalton morreu alguns anos depois disso por pensar que o sinal de transito estava aberto e foi atropelado vivo.

O Átomo

O átomo foi inventado por Demócrito já na esquecida e velha Grécia antiga.

Demócrito, já enfadonhado com o mundo macroscópico, resolve estudar nanotecnologia e entra em uma faculdade de grande renome.

Demócrito sempre foi um homem à frente de seu tempo. Enquanto seus colegas de estudo criavam circuitos lógicos de 3 mícron, Demócrito pensava maior! Alias, menor. Queria criar algo tão pequeno que não se poderia ver.

Um dia trabalhando com um microscópio eletrônico, Demócrito sem querer trocou o fluxo de elétrons para o lado oposto! Isso causou uma reação em cadeia que engoliu todo o seu laboratório subterrâneo. Demócrito por sorte conseguiu sair.

Porem alguns meses depois, após a radiação infravermelho ter sido dissipada, Demócrito retorna ao seu laboratório e observa que em sua mesinha havia varias bolinhas pequenas muito difíceis de serem enxergadas.

Demócrito não sabia, mas havia acabado de criar os átomos!
Átomo são pequenas bolinhas pretas que são formadoras de tudo.

O microscópio eletrônico ao causar a reação em cadeia invés de aumentar a imagem das coisas para podermos ver, ele aumentou as coisas, e não só as imagens. Isso fez com que os átomos, que eram muito pequenos, tomassem dimensões macroscópicas.

Demo começou a estudar essas bolinas e as chamou de átomos. Pois esse era o nome de seu pai, grande filosofo e musico, fez obras belíssimas, como GreensLeeves e Bachianas Brasileiras.

Demo morreu logo depois de câncer por ter ficado exposto a radiação infravermelho, e por infelicidade, Demo não anotou suas descobertas e ficou esquecido no tempo. Sendo retomado mais de dois mil e quinhentos anos depois por Dalton, sujeito esse que tinha um problema nos olhos.

Aprenda Matemática em poucos segundos

Esse é um artigo retirado da revista “Mathematicians and World”, uma revista dedicada ao pensamento matemático em geral.
Esse revista é do mês de maio de 2005 e trata sobre métodos alternativos para se aprender matemática.
O titulo original é “Fermat’s last theorem”. Eu traduzi para o português do jeito que mais se aproximava.


“Desde a época da Grécia antiga o sonho de muitos sempre foi aprender matemática avançada, calculo etc.
O primeiro a fazer o estudo afundo do calculo, tanto diferencial como integral, foi Tales de Mileto.

Tales explicou todo o fundamento do calculo usando semelhança de triângulos. O que, até hoje, é considerado um dos métodos mais simples de se aprender calculo.

Primeira lição: O que é um triangulo?
O triangulo é uma figura geométrica inventada por Platão.
Em seu livro “O mito da caverna” Platão explica toda a sua teoria acerca da formação das cavernas. Ele explica que toda caverna é formada com uma sucessão de triângulos. O que é algo muito inovador para a época. Sócrates foi o primeiro a provar essa conjectura de Platão.
O triangulo é um objeto geométrico que tem 3 ou mais lados.

Segunda Lição: Os lados de um triangulo
Os lados de um triangulo tem 3 nomes. Esses nomes devem ser memorizados.

A, B e C.

Não necessariamente nessa ordem. Ponho aqui uma figura desenha pelo próprio Tales em pele de carneiro.



Terceira Lição: Derivada
A figura abaixo diz tudo e não precisa ser comentada.
O segmento em verde se chama Derivada.



Quarta lição: Calculadoras
É fundamental o uso das calculadoras para efetuar cálculos.
O Primeiro a criar uma calculadora foi Aristóteles, que fez uma versão digital do até então ábaco.


Com essas fáceis lições creio eu que já devo ter sanado todas as duvidas de todos.”

Teoria da geração espontânea

Na Grécia antiga Aristóteles foi o primeiro a querer criar vida.

Vindo de família pobre e humilde, Ari, logo cedo tinha o sonho de criar a vida.
Com o passar dos anos, Ari não passou no vestibular para o curso de medicina que queria, passou vários anos seguidos tentando direito, engenharia e matemática, porem não conseguiu passar em nenhum deles. Já cansado de tudo isso Ari resolve fazer filosofia e passa em primeiro lugar na federal.

Ari gozava do sucesso de ser um vencedor e começou a trabalhar em suas teorias mais mirabolantes.

O Surgimento Da Vida.

Após muito pensar e a nenhuma conclusão chegar, Ari resolve ser pai e criar sua própria vida, deu o nome latino Abiogênese, que diz respeito a criar vida do nada.

Ari, utilizando o seu quite de Alquimia infantil realiza alguns experimentos e consegue criar vida.

Ficou muito famoso na época e as pessoas começaram a chamar ele de O Criador etc.

Mas Ari estava fadado a morrer de uma maneira cruel.

O Rei de Roma não gostou de ter um sujeito criando vida pra lá e pra cá e obrigou Ari a tomar 3 frascos de cicuta sabor limão. Com isso, Ari morreu alguns dias depois.

Sócrates, o filho mais querido de Ari, resolve continuar os estudos do pai, e retoma o projeto do pai e começa a criar vida.

Sócrates escreveu vários textos sobre o assunto e aumentou o discurso do pai. Criou novos métodos de criar vida.
Métodos esses que consistia em apenas pensar. Sócrates criava vida espontaneamente quando queria. Bastava pensar.

Sócrates completou o trabalho do pai e deu, ao seu trabalho, o nome latino Abiogênese, que diz respeito a criar vida do nada.

7 Dicas em como passar no vestibular

Esse é um artigo escrito por Jean Der Vanch, Psicólogo e expert em aprovações. Sua tese de mestrado foi “Metodes de le Vestibule”.

“Uma das preocupações mais preocuposas dos adolescentes dos tempos de hoje é algo que aflige a humanidade desde a época da Grécia antiga.

Le Vestibule

Constituído basicamente de um exame aristocrata que privilegia a classe dominante em seus sórdidos métodos abusivos de governo.
O exame é prestado por adolescente em geral e a principal preocupação é se passarão e a segunda maior preocupação é se não passarão.

Através dessa dissertação proponho apresentar métodos claros e concisos de como prestar um bom vestibular e passar em até no mínimo primeiro lugar.

Primeira Dica: Atenção
No momento de prestação do vestibular é necessária muita atenção. Pode-se adquirir isso facilmente usando alguns métodos de meditação.

Segunda Dica: Atenção
Se você não conseguiu obter atenção até o momento do vestibular; roube-a de alguém que a tenha conseguido.

Terceira Dica: Não estude
É comprovado que estudar diminui suas chances de passar no vestibular e ainda prova que você é burro por não conseguir pensar sozinho. Sem contar o fato que estudar traz problemas sociais ao individuo.

Quarta Dica: Beba muito Álcool antes da prova
É comprovado cientificamente que o álcool aumenta suas habilidades matemáticas, físicas e até extrafísicas. Então não se esqueça de levar seu álcool para o vestibular.

Quinta Dica: Segurança
Se ainda não se sente seguro a respeito do vestibular, contrate alguns seguranças particulares, eles farão que fique seguro com certeza.

Sexta Dica: Aposta
Antes de prestar o vestibular aposte na loteria. É cientificamente comprovado que o ato de apostar em loterias elimina urina no sangue. A urina possui um hormônio chamado Hormonius vestibulares. Esse hormônio, aparentemente sem uso, foi descoberto há pouco tempo pelo russo Kasparov enquanto jogava xadrez. Ele é responsável pela taxa de variação dos neurônios no tempo, ou seja, a derivada do coeficiente de inteligência aumenta com o aumento desse hormônio. Por isso é muito freqüente alunos bebendo urina de seus colegas antes das provas.

Sétima Dica: Final
Se você não esta satisfeito com o resultado final compre 1 quilo de alimento não perecível e faça a matricula em alguma faculdade de boa qualidade.”

Tutorial Hacker

Você sempre sonhou em ser hacker, mas sempre achou demasiado arriscado e não quer ser preso?!

Isso tudo, pois, você ainda não leu este tutorial.
Com ele você aprenderá como ganhar dinheiro fácil, como poderá pegar senhas de seus amigos para bisbilhotas suas vidas pessoais, aprenderá também como fazer um disket explosivo para mandar para seus inimigos fazendo assim com que suas casas explodam e eles percam suas vidas e muito mais.

Lição Número Um: Programas
Um bom hacker deve ter programas hackeres, logicamente.
Um dos melhores programas hackeres desenvolvidos é o MSN Messenger. Muitas pessoas pensam que o MSN é apenas uma ferramenta para conversar com amigos. Mas nunca se perguntaram, por que alguém faria um programa tão inútil e sem utilidade? Ninguém nunca se fez essa pergunta?! A resposta é que ele é um programa hacker disfarçado.
Consiga-o em algum site e instale.

Lição Número Dois: Comandos Básicos e Avançados
Com o programa já instalado deve-se aprender a utilizá-lo de forma correta para melhor aproveitamento.

Comandos que você precisará para as mais diversas operações.

//Dos-Command*...Execute: “Nome do comando”

Todas as formas de comandos a serem executados tem que ter essa forma.
Recomendo aos iniciantes que utilizem o comando “Help” pois com ele se terá uma lista com todos os comandos.
Um dos comandos úteis é:

//Dos-Command*...Execute: Give me Friend Money

Com esse simples comando o MSN consegue acessar o computador de seu amigo/inimigo roubando assim suas senhas. Após isso feito o próprio MSN usa força bruta e testa todas as senhas adquiridas em sites de bancos até um funcionar, coisa essa que demora cerca de 5 minutos. Ao termino do tempo você, usuário do Messenger, já pode acessar sua conta bancaria e ver quando dinheiro adquiriu.

(Nota: O MSN por ser um programa na língua inglesa ira transferir dinheiro em Dólares. É aconselhável que use-se esse comando de acordo com as taxas cambiais)

O próximo comando é o comando para se criar diskets explosivos.
Primeiro adquire um disket e insira em seu computador. Depois entre com a linha de comando.

//Dos-Command*...Execute: Format A: And Create Explosive Disk

O processo de formatação e criação do disco explosivo demora cerca de um minuto. Esse tipo de disco também é conhecido como disco de Boot.
Agora basta dar esse disket a um amigo alegando ser de conteúdo pornográfico ou afins.

(Nota: Após feito o disket nunca o rode! Caso feito isso você corre serio risco de morrer)

Qualquer duvida utilize o comando Help para ter mais informações.

A invenção do dinheiro

O dinheiro foi inventado na Grécia na época das guerras napoleônicas.

Foi inventado por um estilista da moda francês de nome Bernoulli Van Der Graf com o intuito de manipular o sistema político da época. Se as pessoas tivesse dinheiro elas teriam que carregar esse dinheiro consigo para efetuarem transações bancarias. E onde seria armazenado esse dinheiro?! No bolso. Sim. Que malévolo!

Van criou o dinheiro apenas para por mais bolsos nas roupas com o intuito de alegar que a peça tinha mais tecido e custava mais caro.
Van ficou muito rico com isso. Hoje em dia o dinheiro é meramente usado como peso de papel e preenchedores de bolso.

Não se sabe por que, mas a mente humana é tão pequena que o fato de ter um bolso faz com que o cérebro queria enche-lo. Por isso as pessoas trabalham. Para obter mais dinheiro para preencher seus bolsos.

Operações Básicas com Infinito

Nos dias de hoje, é preciso saber mesurar coisas de grandes proporções. O infinito, por exemplo. Sabemos que o infinito é um valor muito aplicado atualmente. Mas suas operações, poucos desconhecem, muitos têm vergonha de afirmar que mexem com o infinito. Vou dar algumas rápidas propriedades do infinito.

P.1) Todo infinito é igual a zero

Demonstração:

Sabemos que

infinito + infinito = infinito

Aqui, se você cortar os infinitos em ambos membros da igualdade, fica:

1 + 1 = 1
2 = 1
2-1 = 0
1 = 0

Multiplica-se agora ambos os termos por infinito:

infinito . 1 = infinito . 0
infinito = 0

P.2) A soma de todos os termos de um infinito é igual a 21

Demonstração:

Infinito = 1 + 2 + 3 + 4 + 5 + 6 + ... + infinito

Sabemos, pela P.1, que infinito = 0. Logo, no segundo membro da equação acima, substituímos infinito por 0:

Infinito = 1 + 2 + 3 + 4 + 5 + 6 + 0
Infinito = 21

P.3) Todo infinito é aproximadamente 357

Demonstração:

Pela P.1, infinito é igual a 0

Infinito = 0

Multiplica-se os membros por 17:

17 . infinito = 17 . 0
17 . infinito = 0
17 . infinito = infinito (novamente P.1)

No primeiro membro, substitui-se infinito por 21, pela P.2:

17 . 21 = infinito
357 = infinito


Podemos generalizar e afirmar que o infinito é uma constante Trial, que vem do latin
Tri - três
Al - tudo
Pois o infinito tem 3 valores distintos, porem iguais em modulo.

Como criar um Vácuo absoluto com pouco dinheiro

Desde a Grécia antiga o homem sonha em criar um vácuo absoluto.
Recentemente esse feito foi conseguido e utilizando materiais muito baratos encontrados em qualquer cozinha.

Você vai precisar de:

· Argila
· Massinha de modelar infantil (cor bonina de preferência)
· 3 litros de água
· 8 benzenos
· Um núcleo de plutônio radioativo tamanho 3

Com os materiais em mãos podemos começar o trabalho. (sempre lembrando que ao manusear plutônio radioativo tamanho 3 use luvas para não ficar exposto a radiação infravermelho)

Passo 1: Com a argila faz-se um chão niveladamente plano. Apenas por questões estéticas. Deixa-se secar por vários dias.

Passo 2: Joga-se água em cima da argila, apenas para o chão ficar com aquela bela cor marrom que agrada a todos nos.

Passo 3: Com a massinha de modelar infantil faça uma peça esférica oca de raio interno e externo de 7 e 5 metros, respectivamente. (lembre-se de que a peça esférica oca de raio interno e externo de 7 e 5 metros, respectivamente deve ser em forma de uma esfera perfeita)

Passo 4: Insira o núcleo de plutônio radioativo dentro da esfera. (Dica, na construção da esfera peça a um amigo para construir ela com você dentro, pois caso contrario será impossível por o núcleo de plutônio radioativo tamanho 3 lá dentro)

Pronto! Está pronto! Em cerca de 5 minutos você terá o seu próprio vácuo absoluto para brincar.

O núcleo de plutônio radioativo tamanho 3 por ser muito volátil, tende a atrair as moléculas de ar para perto de si. Como a peça esférica oca de raio interno e externo de 7 e 5 metros, respectivamente é hermeticamente fechada, nenhum ar de fora vai dar de intrometido e entrar lá dentro para ver o que esta acontecendo.
Com isso o núcleo de plutônio radioativo tamanho 3 vai atrair todo ar da peça esférica oca de raio interno e externo de 7 e 5 metros, respectivamente. Deste modo não sobrará mais nada ao redor.
Você acaba de criar seu próprio vácuo absoluto.
E como você esta dentro da peça esférica oca de raio interno e externo de 7 e 5 metros, respectivamente você pode gozar da sensação de falta gravidade e de não precisar de respirar também.

Nomes de pessoas famosas que tem suas próprias peça esférica oca de raio interno e externo de 7 e 5 metros, respectivamente em seus jardins.

Gauss
Lênin
Euler
BeetleJuice

É tão fácil criar seu próprio vácuo absoluto, não perca tempo.

Guia Prático de Alquimia

Alquimia é a arte de fazer uma coisa virar outra.

A palavra vem de “Alce + Mia”, pois foi a primeira tentativa de alquimia de que se tem relato. Queriam fazer um alce miar, fazendo sua língua de alce virar língua de gato, não se sabe o porquê disso até hoje, mas, enfim.

A alquimia atingiu seu auge na Idade Média, quando todos queriam fazer ferro virar ouro. Muitos alquimistas eram charlatões, sendo apenas enganadores. Mas alguns realmente tinham esse poder.
Recentemente foi encontrado um livro numa tumba egípcia que datava de 3016 A.C., chamado de “Guia Prático de Alquimia em 3 Lições”. Traduzido por 7 Nobels, tal livro se encontra agora no Museu Internacional dos Tomos Raros (MITR). Os procedimentos básicos de como se tornar um alquimista foram divulgados pela Internet:

“Como se tornar alquimista

Passo 1: Você precisa de uma sala escura, arejada, que tenha água corrente, bem iluminada, e sem corrente de ar. Essa sala será chamada de A Sala do Alquimista. Ah, você também precisa de traje a rigor.

Passo 2: Ache um gato.

Passo 3: Ponha o gato na corrente de água, pegue um fio desencapado, ligue na tomada uma ponta e a outra na água.

Passo 4: Você agora tem um belo gato empalhado. Ponha esse gato na sua escrivaninha, ele será útil em momentos de falta de inspiração.

Passo 5: Pegue um pedaço de ferro.

Passo 6: Pinte de amarelo.

Passo 7: Fale que é ouro e venda para os trouxas.

Passo 8: Nos passos de 5 a 7 você transformou ferro em dinheiro, isso é um sinal de que você está progredindo.

(...)”

Provando a inexistência do Ar

Na Grécia antiga as pessoas acreditavam em varias coisas, uma delas era o ar.
A criação do ar aconteceu no Século VII com o romano Alexandrius Arnius. Filosofo e alquimista.

Defrontando com uma pergunta de um de seus discípulos:

“Suponha que o individuo X esteja próximo ao mar. Ele sentira uma força atuando contra si. O que é essa força?”

Depois de décadas pensando AA finalmente conseguiu uma resposta para isso.
Criou uma entidade que autodenominou de ar.
Essa entidade teria massa e obedeceria ao principio de incerteza de Newton.
E em regiões próxima dos mares esse suposto ar estaria em movimento devido a uma força maior.

Discussões ao redor do mundo foram travadas sobre a inexistência e a existência do ar. Pois os argumentos eram falhos.

Como poderia existir algo que tem massa, atua força, e eu não vejo?!

O químico russo Kepler provou que o ar não existe fazendo o seguinte experimento.

Pegou 3 litros de acido sulfúrico com 1 dente dentro, 700 mililitros de água e um béquer vazio.

Se o ar existisse e tem massa ele poderia ser coletado. Então com o béquer e com a ajuda de uma bomba ele colocou uma porção do suposto ar no béquer.
Fechou hermeticamente para não entrar ar. Jogou acido sulfúrico e água.
Isso resultou em uma explosão enorme e Kepler perdeu 1 braço.
Com conclusão Kepler deixou o seguinte.

“O ar não existe, se existisse todo o mundo já teria explodido”

Por que as cordas do violão são mais grossas em cima e mais finas embaixo!?

“Por que as cordas do violão são mais grossas em cima e mais finas embaixo!?”

Essa é uma pergunta que aterrorizou muitos homens e amedrontou outros desde os tempos vulcânicos. Primeiramente, vamos lembrar como apareceu o primeiro violão.

Klunch, homem esse do tempo das cavernas, estava caçando seu mamute com uma clava. Ao achar um mamute, ele furtivamente chegou perto do animal e lhe socou a clava. Mas, ao errar a mira, ele acertou apenas o chifre do bicho. Isso fez com que a clava se partisse e tomasse a forma do que conhecemos hoje como violão.

Klunch, amedrontado por estar sem arma, correu em disparate, chegando à sua aldeia. Jogou sua “ex-clava” no lixo e foi dormir. Seu filho Klump achou aquele pedaço de clava engraçado por diversos motivos e decidiu guardar o mesmo para futuramente brincar de bangue-bangue, porque aquilo se assemelhava a uma espingarda.
Mas, repentinamente, Klump teve uma idéia brilhante:

Por que não colocar fios na clava e tocar uma doce melodia?!

Bem. Não se sabe até hoje como ele teve essa idéia. Só sabemos que Klump pegou vários fios de diâmetros diferentes e amarrou na clava. O curioso é que, independente da ordem em que ele colocasse os fios, eles no final se reorganizariam automaticamente ficando os mais grossos em cima e os mais finos embaixo.

O primeiro a desvendar esse evento foi Fermat, que enunciou o seguinte:

“A distância que separa uma corda grossa da outra ligeiramente menos grossa é tal que essa distância é mínima”

Ou seja, cordas de diâmetros próximos tendem a estar próximas umas das outras. Isso explica o porquê de elas estarem assim agrupadas.
Mas, por que as mais grossas ficam em cima e as mais finas embaixo? Isso só foi descoberto por Albert Einstein, quando viu sua mãe costurando seu macacão e ouviu a vibração da linha de costura e concluiu:

“A gravidade em baixo é logicamente mais alta que em cima, logo para as cordas terem o mesmo peso, as de baixo tem que ser menores e mais finas, para compensar com o volume e para a densidade ser a mesma”

Agora a humanidade já dorme tranquila sem ter que pensar nesse dilema

Chuva

Há pouco mais de dois séculos o homem moderno inventou a chuva como meio de irrigação de lavouras de cana de açúcar.
Porem, o uso continuo da chuva pelo homem causou grande perturbação na mãe Terra, causando eventos climáticos inesperados. Um desses eventos é a chuva.
Essa chuva é muito diferente da chuva. Por dois motivos, ela não serve para irrigação de lavouras de cana de açúcar, muito pelo contrario, ela não tem utilidade.

E uma das perguntas mais antigas que o homem se faz é “Como não me molhar na chuva?”.

Um homem engenhoso, Grand Bell, propôs a resposta para essa pergunta e inventou assim o telefone.
Mas para a tristeza de todos essa invenção não fez com que o homem parasse de se molhar na chuva.

Alguns filósofos afirmaram que quando se esta na chuva na verdade você não esta se molhando, você esta apenas enxergando a realidade de um mundo superior. E lógico que tais filósofos já foram queimados em fogueiras há muitos séculos.

Porem. Isaac Newton no famigerado século XVIII inventou uma equação para não se molhar na chuva.

Ele abriu mão de uma coisa chamada referencial, que diz respeito de como o mesmo evento estaria sendo enxergado pela visão de outro ser localizado em um certo ponto.
Assim ele trocou os referenciais. Não era mais a chuva quem caia, mas a gente que subia.

Ao andar estaríamos nos deslocando em relação à chuva fazendo um ângulo theta com a normal. Esse ângulo aumentava, obviamente, com o aumento da velocidade.

Newton disse que só havia duas soluções para esse ângulo ser zero, ou você corria na velocidade da luz e aplicaria formulas da relatividade restrita, por que já que você esta se deslocando a velocidade da luz, o tempo de exposição a chuva seria 0, assim não se molharia. Ou a outra solução, você ficaria parado. Por que parado você não teria velocidade, e quando mais rápido mais se molha, de acordo com a formula de Newton.

Assim se você ficar parado na chuva você não se molha, o ângulo entre você e a normal será zero.

Newton escreveu o livro “Can I always be wet?” e ganhou 3 prêmios Nobels.

A velocidade da Luz é enganosa

Não se deixe enganar pela velha lorota que diz que a velocidade da luz é bem rápida.
Na verdade, a velocidade da luz é um dos meios de transporte mais lentos que já existiu.

Retornemos ao passado, na época da Grécia Antiga. Os grande pensadores pensaram que, se você tem uma fonte de luz F1 no ponto A, e lá na frente uma outra fonte de luz F2 no ponto B, e a distância entre A e B é x, a velocidade da luz que emana de F2 será logicamente maior do que a de F1, pois está sempre à frente dela. Como, basicamente, a velocidade da luz é a mesma, e F2 está à frente, logo F1 nunca chegará a F2.

Portanto, se ele nunca chegará, podemos enunciar que a distância entre os dois é infinita. Porém! Se no início a distância era x, e depois virou infinito, e as velocidades iniciais eram as mesmas, logicamente a aceleração de F2 é infinita ao quadrado. O que faz com que seja bem rápido. Essa luz realmente corre em disparate.

Como os gregos explicaram tal fenômeno?!

Bem. Platão, que descobriu tal coisa primeiramente, chamou isso de “O Mito da Caverna”, porque ele viu isso quando estava devaneando numa caverna e reparou que a luz que corre para dentro da caverna é bem mais rápida do que a que entra, é tão rápida que nem a enxergamos. É por isso que vemos apenas uma escuridão, porque de tão rápida a luz nem ilumina as coisas da caverna.

Passam-se dias depois dessa fenomenal descoberta e chegamos aos dias de hoje. O que hoje chamamos de “ano-luz” é apenas uma pequena graduação da régua que mede 1 segundo de viajem da luz descoberta por Platão. Por isso, meus amigos, não se deixem enganar pela tediosa luz comum e lentíssima.

Como achar raízes de um polinômio de grau nove ou superior

Uma das coisas mais difíceis em exatas é achar raízes de polinômios com grau nove ou superior, justamente por que essas raízes estão muito bem enterradas na mãe Terra e serem muito grandes.
Porem, ao contrario do que muitos pensam, esse é um processo bem fácil e rápido.

Vou provar, por contradição, rapidamente que a raiz de qualquer polinômio de grau superior a nove é exatamente um. Ou seja, todo polinômio de grau muito grande tem suas raízes convergindo para o numero um.



Vamos então começar aprova por contradição.
1 é a raiz do polinômio, como queremos provar, então falemos que 0 é a raiz, se zero no for, então 1 será. Jogando f[0].



O que desmente a nossa conjectura anterior. Então por contradição, a raiz de todo polinômio de grau superior a nove é 1.

O Álcool e o Homem

Desde os primórdios da sociedade romana o homem e o Álcool tem sido bons amigos.
Mas recentemente, por causa do aumento da entropia do universo, devido à teoria do caos, o homem e o Álcool perderam um vinculo de amizade. Tendo somente agora uma amizade parcial.

O Álcool é formado por 6 carbonos, 12 hidrogênios e +/- 7,3 carbonos.
Lembrando aos que tomaram recuperação em química que essa é a mesma formula da água.
Por isso o Álcool é transparente e liquido ao mesmo tempo, em física chamamos isso de dualidade.

O Álcool, por ser volátil, tem grande capacidade de entrar rasteiramente no metabolismo do homem, sem que o mesmo perceba. Isso acontece por via oral, mas pode acontecer também por outras vias não tão usuais assim.

O processo de ingestão do Álcool acontece basicamente em duas etapas, a etapa 1 e a etapa dois, para facilidade de compreensão chamá-la-emos de E1 e E2, respectivamente.

E1 é caracterizada pela entrada de liquido no organismo indo parar diretamente nos rins, lugar esse onde é fermentado as gorduras presentes no Álcool.

A E2 acontece no cérebro, onde essas gorduras já fermentadas vão. Estando já no cérebro essas gorduras fermentadas atuam em um processo chamado sinapse eletrolítica, que diz respeito ao fluxo de elétrons entre os neurônios do cérebro. O Álcool atua como um catalisador, fazendo com que as sinapses eletrolíticas aconteçam mais rápido.

Por isso que é essencial beber antes de dirigir, porque deste modo o sujeito estará com sinapses eletrolíticas tão velozes que ele poderá até prever o futuro, dependendo do grau de Álcool ingerido.
Os Farmacêuticos receitam 1 grama de Álcool por neurônio eletrolisado.

Pesquisas medicas avançadíssimas provaram que quem bebe vive mais e vive mais feliz também. Já que uma porcentagem do Álcool ingerido não é fermentado, e essa porcentagem vai para os músculos. Fazendo assim pequenas massagens neles, fenômeno esse chamado de massagem celular, causando uma sensação de prazer.

O Álcool pode e deve ser ingerido por pessoas com mais de 0 anos de vida e o limite de idade tende a infinito. Sendo aconselhado para todos os tipos de pessoa. Pois o Álcool não exclui classe social, cor e religião.

Evolução

A que ponto chegará a evolução?! Bem. O processo de evolução é complexamente entendível. Sabemos que os elétrons evoluíram para prótons, que evoluíram para átomos, que evoluíram para moléculas, com n tendendo a infinito até chegarmos no universo. Um exemplo clássico de evolução também é o geométrico. Se você arrasta um ponto ele evolui para uma reta, se você arrasta a reta ela evolui para retângulo, e arrastando o retângulo ele evolui para um paralelepípedo, e assim por diante, todos sabemos o que vem depois.
A questão é. Como acontece a evolução?!

Simples. Segundo o evolucionista ucraniano Kriev Kriegger Hausben, todos os seres vivos (defina-se aqui “ser vivo” como todo e qualquer ser que possui coeficiente elétrico) possuem uma substância chamada de Ciclometilato de Evolutila, que auxilia na evolução. O processo é simples: esse composto, por ser muito volátil, sai do ser vivo por osmose e aflui pro meio, deformando o espaço e conseqüentemente adaptando tal espaço para melhor aconchegar o ser vivo.
Ou seja: o processo evolutivo não adapta o ser vivo ao ambiente, e sim o ambiente ao ser vivo, o que contraria evolucionistas tradicionais como Darwin e Kriegger Hausben.

Tomemos como exemplo a Drozophila melanogaster, vulgarmente conhecida como “mosca de fruta”. Se ela quer comer, por exemplo, uma banana, e seus dentes não são grandes o bastante, ela rapidamente libera o Ciclometilato de Evolutila, que, ao invés de aumentar seus dentes, diminuirá a banana. É por isso que muitas vezes olhamos embaixo da cama e achamos várias pequenas cascas de banana. Às vezes também as encontramos em cima da geladeira, dependendo de onde a mosca esteve.

Mas. Como que o Ciclometilato de Evolutila atua?! O químico francês Dejardi Von Jabur nos explica em seu recente livro:

“(...) e o Ciclometilato de Evolutila é muito constriburente. Ao entrar em contato com, por exemplo, uma banana, ele faz com que suas células dividam-se por duas moléculas (...) sobrando assim um número primo de átomos, número esse bem pequeno (...) o que reduz drasticamente a massa da banana. O que sobra transforma-se em energia quântica...” (Von Jabur, Dejardi. In: ‘Evolutila & Sociedad’)

Bem. Acho que depois disso tudo fica claro que os homens são derivados diretos dos moluscos articulados.

Gol

Recentemente aconteceu um fato histórico que marcou a humanidade por vários séculos.

O brasileiro Calos Drummond de Andrade, celebre inventor do avião e também fã de futebol, criou uma empresa de nome GOL, em homenagem a sua aficção por futebol e seu hobbie em aeromodelismo.

Com o passar dos séculos essa empresa foi ficando de grande renome e Cal foi ficando cada vez mais rico, e com a invenção do capitalismo por Carl Maxwell, Carlos começa a fabricar aviões de pouca qualidade, com o intuito de ganhar mais dinheiro.

Há poucos dias atrás um avião da Gol se dirigia para o ponto x. Foi quando, no ponto x – y, houve um defeito mecânico!

As assas do avião, comumente chamadas de Assas, rasgam velozmente o céu a uma altitude muito alta, como se é esperado. E lá no céu o ar é muito frio, por causa do enorme vento causado pela rotação da Terra em torno de seu eixo.

O ar a essas altitudes é tão frio que as moléculas de ar começam a tremer com o intuito de se aquecerem. A assa do avião por ser retrátil começa a tremer também, causando um fenômeno que os metafísicos chamam de Turbulência.

O avião, por viajar a uma velocidade próxima a da luz, curva o espaço formando um circulo de raio unitário.

O avião, seguindo a trajetória do circulo acabou colidindo com a mãe Terra, causando uma enorme explosão que até hoje é escutada pelos astrólogos. Em homenagem as pessoas mortas, essa explosão foi chamada de Big Bang, que vem da língua latina neo romana “Saudosas Lembranças”.

Carlos ficou tão triste com isso que resolveu abandonar o aeromodelismo e passou a escrever poemas.

Paradoxo dos gêmeos

Esse é um paradoxo que intrigou varias mentes da humanidade moderna por milênios.

Consiste no seguinte.

Tem-se dois gêmeos com 10 anos de idade, para fins explicativos vamos chamá-los de G1 e G2. Põem-se os dois gêmeos dentro de uma espaço-nave e eles saem em disparate com uma velocidade próxima a da luz por 30 anos.
Quando eles voltarem, como saberemos quem é G1 e quem é G2?
Já que eles ficaram 30 anos viajando estão trinta anos mais velhos então é quase impossível saber quem é quem.

A probabilidade de G1 ser G2 é astronômica, um numero de mais de 5 casas decimais!!
Um judeu de nome Albert Einstein propôs a resposta para esse problema.
Após vários gêmeos de laboratório perderem sua vida pela causa, Einstein disse a celebre frase.

“Tudo é relativo, não importa se você esconder um gêmeo ou outro gêmeo, a questão é que sempre haverá um referencial para o qual você escolheu o gêmeo certo”

Einstein morreu logo depois que disse tamanha idiotice, e os pensadores da época resolveram por nomes nas roupas de astronauta para acabar com o paradoxo.

Critérios de Divisibilidade por zero

Desde os tempos remotos o homem vem escondendo seus segredos da humanidade.

Um caso claro e verídico disso aconteceu na Grécia com um senhor de alto porte e que usava o nome Pitágoras.

Esse sujeito, mesquinho por natureza, trabalhava com seu seleto grupo de capatazes, chamado de clã.

As descobertas mais brilhantes da humanidade naquela época aconteciam e ninguém tomava conta disso.
Por milênios Pitágoras escondeu seus estudos científicos.
Pessoas nasceram e morreram sem saber a verdade.
E após muita relutância, Pitágoras não é vencido e um de seus discípulos consegue publicar a Temida Formula De Pitágoras em um jornal de grande publicação da época.

Na rua as pessoas apenas comentavam aquele feito e menosprezavam o pequeno Pit por ele não ter dividido suas grandes idéias matemáticas com os outros.

Hoje em dia todos dizem “Globalização, Impressa” e algumas outras besteira.
Mas elas nem desconfiam que as grandes mentes do mundo ainda temem em esconder seus segredos e enganar a humanidade apenas para o seu gozo próprio.

Um caso mais marcante desse fato foi o da constante imaginaria.
Muitos professores do Séc XVII sabiam da existência dessa constante através de textos da antiguidade.

Porem, com o intuito de favorecerem a si mesmo com essa maravilha do i, acabaram escondendo isso dos seus mais queridos alunos e falando que não existe raiz de numero negativo.
Agora a pergunta, por que as mentes brilhantes escondem o segredo das coisas para a humanidade?!

Isso tudo começa na maçonaria, o berço do conhecimento cientifico da humanidade.

Criada na época do Egito pelo faraó Ramsés.
Era uma sociedade patriarcal que tinha como base o pensamento humano.

Porem, por perceberem que estavam trabalhando com algo de bastante importância e perigoso, acabaram se disfarçando de bons cidadãos fumantes de charuto cubano e que tinham reuniões para discutirem sobre política e ocultismo.

Nesse novo século XXI vários segredos foram desmascarados deles e posto a publico, como a prova irrefutável que Jesus era negro e era parente de quinto grau do Deus todo poderoso.
Mas... A alta classe maçom ainda insiste em deter um conhecimento, considerado o mais poderoso de todos. Pelas estipulações crê-se que apenas 7 membros retém esse conhecimento.

A divisão por zero.

Tida como a mais difícil operação matemática por uns e como impossibilidade numérica para outros.
Mas os maçons há mais de 3 mil anos descobriram como efetuar tal calculo de uma maneira bem simples e estabeleceram varias regras de divisibilidade por zero.
Uma das quais irei explicar aqui.

Tem-se um número na forma abcdefg... com n casas. Ele será divisível por zero, se e somente se o índice da permutação logaritma for um numero divisível por zero.

Com essa regra básica é possível provar vários postulados como a Constancia da velocidade da luz.

A Divisão por zero é ainda algo que fascina crianças e deixa a todos curiosos.

Utopia

Desde os primórdios da civilização humana, os seres vivos, e os mortos também, tentam criar um modelo de sociedade perfeito, tudo isso em vão até então.

Porem, recentemente, com bases nos textos do sociólogo Alemão Dutch Heinzer, que prova que a integral dupla da função evolução humana em função do tempo e do nível intelectual da época, tende a uma constante. Conhecida como constante de estabilidade utópica.
Seu valor é aproximadamente 1.000 com 4 casas decimais de precisão.
É visualmente visível que esse modelo adotado por But. é um modelo falho e cheio de falhas. Com uma mera precisão de 4 casas, uma precisão Tetra-casal, ou ButCasal, como é chamada pelos químicos, ao longo de varias interações, infinitas essas, a precisão Tetra-casal tende a uma reles precisão Meta-Casal, ou seja, de uma casa.

Muitos indivíduos ainda tem a dificuldade de perceber que a constante de estabilidade utópica é um numero diferente de 1, pois 1 é um numero natural, já a constante utopia não é uma coisa tão natural assim, ela é vista apenas em sociedades avanças, em que pessoas usam anéis.

A dificuldade na precisão dos cálculos da constante decore pela não fluabilidade do tempo, ou seja, o tempo não é continuo, sendo assim não se pode integrar usando qualquer t, tem que se usar apenas valores de t que pertencem à partição fracionaria do tempo. O que até hoje não é muito bem entendido pelos físicos do mundo.
Porem, apesar de todas as controvérsias do assunto, os valores analisados por But são os melhores da época.

Se por exemplo, jogarmos 1 na equação de But teremos como resultado 1.000.

Podemos provar por indução magnética que se jogarmos 2 teremos como resultado 1.000.
Porem os valores para 3 e 4 ainda são um mistério para a sociedade ocidental.

Concluímos esse texto afirmando o fato principal, uma mera precisão But-Casal não é de longe uma precisão precisa ao pe da letra.